中国脅威論

　いろんな人がいろんな場所で、中国の脅威について書かれています。今更何か新しいことが書けるのか分かりませんが、設計者が中国をどう見ているか、今の時点での見方を書きたいと思います。

　設計者が中国を利用する理由は、人件費が安いからです。日本の五分の一と言われるその安さだけが、中国の魅力です。中国の組み立て工場では、人がトランスファーマシーンのように並び、トランスファーマシーン並みの単純作業を繰り返しています。ホントに一つの部品をねじ止めしたら、次の人に渡すという単純作業です。日本では、２、３人で出来そうなことを１０数人で一つのラインを作り、組み立てを行っています。何故か、それは作業者一人一人が定着しないからです。全ての作業者が数カ月で辞めていくそうです。しかし、工場の外は仕事を求める人があふれていて、安く若い労働者をいくらでも雇えるそうです。つまり来たばかりの若い人に、直ぐ出来る様な作業しかさせられないということです。それで、安く作れるのです。

　中国もそんな粗悪品ばっかり作っているような工場ばかりでなく、きちんとした技術を持ったメーカーもある。と、よくニュースでコメンテーターが言ったりしています。「日本もうかうかしていられませんね。」と締めくくられます。確かに、高い技術力を持ったメーカーも中国にあります。しかし、そこは高いのです。そりゃそうです、日本で作られた工作機械を輸入し、その高度な機械を使える優秀な人材を使っているからです。そしてその優秀な人材はかなり人件費が高いのです。製品のコストは、人件費、設備費、材料費、利益、で決まります。設備費は日本から輸入しているので、変わりません。材料費は、微々たるもんです。人件費、今まで安かった人件費も、優秀な人材を確保するため高くならざるえません。結局、中国からの輸送費など考えると、高い技術力を持ったメーカーと取引する、メリットが無くなります。設計者は安いところをどう使うか、今も考えているはずです。
　中国の高い技術が脅威となるためには、世界の工場と呼ばれ、安い労働力を海外のメーカーに提供する段階ではだめで、独自の高い技術力を生かした製品を開発した時になるでしょう。

　現在の中国脅威論は、中国のリスクに移っているようにも感じます。このまま中国で生産し続けることが出来るのか、政治体制は安定なのだろうか、対日感情は？、そう言ったことや、徐々に上がる作業者の給料などもあり、中国から東南アジアへ工場が移っているようです。日本から工場がどんどん遠いところへ移ってしまうのでしょうか。韓国→中国→東南アジア→インド→中東へ。
　日本は相変わらず不況です、工業は海外に移転してゆき、経営者も技術者も海外へ出て行ってしまいます。雇用は生まれず、安さを求める流れは、変わらない。どこかで、日本に流れを引き戻さない限り、日本からモノ作りが消えてしまうのでは無いでしょうか。ありがたいことに、Made in Japanという神話はまだ生きています。高くても信頼性ある製品を求めてくれる人に向け、Made in Japanをアピールする製品やメーカーが多く出てきてくれると、私も仕事先を見つけることが出来るかもしれません。

グラフマニアチュートリアル８ シート構成

 　”使用説明書”シート



　使用方法の書かれたシート。

”データー”シート



　データーを貼り付けるシート。”３”行目に見出しが来て、”４”行目以降はデーターが並ぶようにしてください。張れるデーターの大きさは、横に５０列、縦に１０００行です。最初は、その範囲に枠線が表示されています。ピボットテーブルでは、１行または１列間隔が空いていると処理してくれませんが、このファイルはお構いなく処理します。データーが有ろうと無かろうと、横５０列縦１０００行を集計しているためです。

”見出し”シート

　データーを分析し、フィルターや凡例に使う見出しを抽出しています。C14～BA1013の範囲で、重複しないデーターの数を数えています。データーが１０種以下の場合、フィルターや凡例に使用できる項目と判断します。C2～BA12まではフィルターに使用するデーターを抜き出しています。B5～B54までは軸の項目選択用のリスト、B56～B105は凡例とフィルターの項目選択用のリストになります。

”散布図”シート

　グラフ下のB5～B1004までが横軸、C5～C1004までが縦軸の一次抜き出しになります。それぞれB4、C4の表示項目と合うデーターを、”データー”シートから参照しています。B4,C4はドロップダウンリストとリンクしています。D5～M1004までが実際グラフにデーターを表示している範囲になります。凡例で項目を指定していると、”データー”シートを参照して凡例が一致した場合のみ、一次抜き出ししたデーターを参照表示しています。D列のみD4が空白表示だった場合、全てのデーターを一次抜き出しから参照表示するようにしてあり、凡例が無指定だった場合全てのデーターを単一の色で表示できるようになっています。O3～O12はフィルターを指定するときに参照する、ドロップダウンリスト用のリストです。ドロップダウンリストは参照する場所を、関数で変える事が出来ないので、表の方でデーターを入れ替えるようにしています。グラフに表示されるD5～M1004の範囲では、フィルターの表示がある場合は、データーを参照して一致する場合だけ、データーを表示するようにしています。（IF関数が二重に掛かっている）

　表示しないようになっていますが、C５～C1004もデーターをプロットしています。凡例のマーカー指定で表示しないようになっているだけです。これは、フィルターを掛けた場合、グラフの表示範囲（軸の表示）が変わってしまい、表全体が書き変わるため変化が分かりにくくなってしまう為です。

”度数分布”シート

　”度数分布図”シートは表の構成はほぼ”散布図”シートと同じです。軸を２つ指定する必要がないので、”散布図”シートの横軸データー参照が無いです。度数分布なので、R43～AB54で個数をカウントしています。フィルターや凡例の処理はC5～L１００４で行っているため、R43～AB５４ではその範囲のデーターの数を数え上げているだけになります。

　フィルターを掛けると、表示範囲が変わってしまいます。もし表示範囲を固定化したい場合P43～P54を描き変えてください。

　散布図だけでなく度数分布を作ったのは、生産現場などで調整が上手くいっているか簡単にわかるからです。散布図では調整値がどれくらいの幅で管理できているのか、同じ場所に複数プロットされたりして理解できません。

グラフマニアチュートリアル７ 凡例とフィルター

　調整要素AとBの調整値を決めて、再度１０台製品を作ったところ、全て合格した。新しく製造したものをフェーズS2として、データーの方へ追記してみます。

調整値を決めて製造した製品データー

11	S2	9.94	3.40	5.80	96.2	合格
12	S2	8.75	4.22	3.22	89.9	合格
13	S2	9.83	4.42	3.03	99.8	合格
14	S2	9.24	5.49	3.80	95.1	合格
15	S2	9.14	5.89	6.31	94.1	合格
16	S2	9.56	3.35	8.87	93.5	合格
17	S2	9.44	3.96	2.20	93.8	合格
18	S2	8.82	5.88	9.82	93.1	合格
19	S2	9.93	3.84	5.64	99.1	合格
20	S2	9.17	3.41	5.60	89.4	合格

　”散布図”シートを表示し、縦軸を”評価”、横軸を”調整要素A”、凡例を”フェーズ”にすると、フェーズ別に色分けされた、データーの分布を見ることができます。

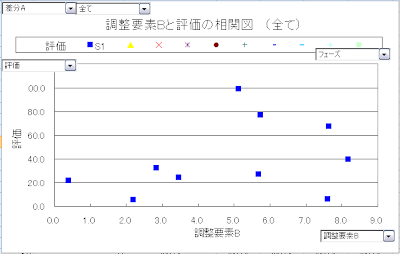
　又、縦軸を”調整要素B”に凡例を”合否”にすると、合格した製品の調整要素ABの座標での分布を確認できます。これは、データーが多く集まっている時に２つの要素がどう影響し合っているかを確認できます。下のグラフは、無調整で８０台組み立てた時の合否の分布です。

　データーが増えてくるとこんな関係も見えてきます。これによると、調整要素Bは2～8まで範囲を拡げられるかもしれません。

　フィルターを使うことで、合格したデーターだけ表示させることもできます。下のグラフは凡例を”フェーズ”にしフィルターを描ける項目を”合否”、その中から”合格”だけを表示した例です。

　データーが多く複雑になってくると、ある特定の条件だけ抜き出して、見てみたいということも出てきます。実際の業務で扱うデーターは、こんなに単純ではないと思います。その複雑なデーターから、関連性を見つけ出す手助けになれば幸いです。

グラフマニアチュートリアル６ 近似曲線を多項式化する

調整要素Bと差分Aのグラフでは、山なりのデーター分布が見られましたが、直線の近似曲線では、全く近似できていませんでした。そこで、近似曲線を多項式化してみます。ｘの２乗や３乗に比例するという中学生の時に習ったやつです。カーソルを近似曲線に合わせて右クリックをします。この時、他の場所を選択してしまうことがありますので、近似曲線を選択できるまで何度もやり直します。選択できると、”近似曲線の書式設定”というポップアップメニューが出てきます。それを選択します。

多項式近似を選択し次数をいじります。次数を大きくすると複雑な曲線が描けるようになりますが、そのような相関関係がありうるのか、慎重に判断する必要があります。基本的になるべく単純な次数の低い近似曲線を描くようにします。

今回は次数２で描かせました。

調整要素Bを３～６の間で調整できれば、差分Aを５～１０±５位に抑えられそうです。つまり調整要素Aで評価を８０点以上にすれば、調整要素Bとその他の要素で０～１５点プラスされるので、全ての製品を合格にすることができるかもしれない。調整要素Aで評価を８０以上にするためには、前に出てきた近似曲線の式を逆算して、８．７以上にすれば良さそうです。

調整要素Aを８．７以上に管理することが難しい場合は、さらに調整要素Cがどんな影響を及ぼしているのか確認するか、調整要素Bの調整幅を狭くするか、手を考えないといけません。実際の製品においては、調整するための手間やコストを考えて、最適な調整幅を決めることになるでしょう。

また今までの解析結果が全面的に正しいとは限りません。かならず、追試をして上手くゆくことを確認する必要があります。

グラフマニアチュートリアル５ 差分を取ってみる

　差分の取り方は簡単です。評価から数式分を引けばいいのです。”データー”シートを表示し”合否”の隣の列に”差分A”と見出しをつけ、下のセルに”=F4-8.7005*C4-4.7459”を入力します。F列が”評価”C列が”調整要素A"とします。

　これをデーター分下にコピーすればデーターの用意は終わりです。”散布図”シートに戻り縦軸を”差分A”にしてみましょう。

　調整要素Aの影響を取り除いているので、横軸が”調整要素A"の時は当然相関がみられません。横軸を調整要素BやCにしてみましょう。

横軸を調整要素Bにしたグラフ

横軸を調整要素Cにしたグラフ

　調整要素Bにした時には、データーの分布が５付近で盛り上がっている山形になっています。調整要素Cの方は、ランダムな分布で傾向が分かりません。評価と調整要素Cの時には右下がりの相関があるように見えましたが、差分Aとのグラフでは相関が見られなくなってしまいました。データーが少ない場合は、関係がありそうに見えてしまう場合があります。

　調整要素Bの方は、今まで見えてこなかった関係が見えてきました。これはより大きな影響を及ぼしていた調整要素Aを取り除いたため、調整要素Bの影響を確認できるようになったのです。調整要素Bの影響を取り除けば、調整要素Cの影響を確認出来るかもしれません。

グラフマニアチュートリアル４ 近似曲線を表示する

 　グラフの横軸を調整要素Aにもどし、近似曲線を追加します。グラフの青いマーカー上で右クリックをすると、ポップアップメニューが表示され、その中から”近似曲線の追加”を選択します。

　”グラフに数式を表示する”と”グラフにR-2乗値を表示する”のチェックボックスをチェックします。

　これでグラフ上に近似曲線の数式とR２乗値が表示されます。R2乗値は１に近いほど、データーが近似曲線に近いかを表しています。ちなみに、横軸の表示を”評価”にすると、R2乗値が１になります。

　数式によると、調整要素Aを8.65以上にすると評価で80以上になりそうですが、データーのばらつきがあるため、それだけで全てを合格にすることは出来そうもありません。調整要素Aを10に固定できたとしても、91.7点にしかできず、データーのばらつきの方が１０点以上ありそうなので、全てを合格にすることは無理そうです。

　そこで近似曲線との差分をとってみます。差分とはデーターと近似曲線との差のことで、これにより、調整要素Aの影響を排除した形でデーターを見ることができます。

　つまり、表示された近似曲線を調整要素Aの理想的な評価への影響とみなし、差分を取ることで調整要素Aの関与を無くしてしまおうということです。なんというか、そんなに上手くいくのか、と思うような強引な手段ですが、気にしない。

グラフマニアチュートリアル３ 散布図を見てみる

 

　まずは、評価の項目を縦軸にし、横軸を調整項目のどれかにします。グラフ作成の基本として、横軸に原因となる項目、縦軸に結果を持ってくるの原則です。凡例はフェーズを選んで下さい。

　調整要素Aを横軸にしたときのグラフ。

調整要素Bを横軸にしたときのグラフ。

調整要素Cを横軸にしたときのグラフ。

　ざっと眺めてみると、調整要素Aと評価の間に明らかな相関がみられます。相関関係があるというのは、散布図のデーターが、一本の線の様に分布していることをいいます。これはy=f(x)の関係が成り立っていることを示唆しています。多少のバラツキは、他の要素の影響か誤差と考えられます。もちろん、軸の表示範囲によっては、下二つのグラフも一本の線の様に見えることになります。縦軸を１０倍の範囲で表示させれば、一本の横線のように見えるでしょう。しかし、横線はy=f(x)の関係ではなく、y=aを示しているだけです。xとの関係（相関）は伺えません。幸いこのグラフマニアでは、軸のスケールは自動で調整されますので、気にする必要はありません。

　一番上のグラフは、胡散臭いくらいの相関具合ですが、とりあえず調整要素Aが評価に対し大きな影響を持っているようです。調整要素Bとは相関がみられず、調整要素Cとはマイナスの相関があるように見えますが、どうでしょう。

グラフマニアチュートリアル２ データーの説明

　表１．のデーターは、今一性能の安定しない製品を１０個製造した時の物です。A、B、C３つの調整項目があり、その性能を１００点満点で評価し、８０点以上の性能で出荷OKとします。調整項目はそれぞれ0～10までの無段階です。

表１
製造番号	フェーズ	調整要素A	調整要素B	調整要素C	評価	合否
001	S1	8.00	7.63	6.33	67.5	不合格
002	S1	5.16	8.17	9.46	39.3	不合格
003	S1	0.45	2.18	4.57	5.4	不合格
004	S1	1.41	3.46	8.35	24.5	不合格
005	S1	3.05	2.84	7.07	32.7	不合格
006	S1	3.89	0.38	4.18	21.4	不合格
007	S1	7.34	5.72	5.05	76.9	不合格
008	S1	1.18	5.67	8.92	28.0	不合格
009	S1	9.83	5.12	1.47	99.0	合格
010	S1	0.29	7.59	6.87	6.0	不合格

たった一つしか出荷基準を満たせませんでしたが、とにかく、製造番号のところから一番下の不合格のところまでを、グラフマニアの”データー”シートに書きこみます。元々あったデーターは消してください。
　表１．のような形式の表を、マイクロソフトはデーターベース形式の表と呼んでいます。一覧表といった方が、解りやすい気がしますが、それより厳格な規則があります。

グラフマニアチュートリアル１ 前置き

　グラフマニア.ｘｌｓを投稿してしばらく経ちましたが、自分の思っている以上にダウンロードして頂いているようで、驚きです。ありがとうございます。ベクターのランキングは大したことありませんが、こんな、ピンポイントな物をこれだけの人に必要としてもらえるとは、うれしい限りです。失業中なので、こんなことでも無いと、自分はいらない人間なのかとネガティブになってしまうので。

　前置きはその辺で、せっかくダウンロードしてもらっても、使い方がわからない。あるいは今一どう使ってよいのか解らない、という人もいるかもしれません。操作自体は大したことはなくても、仕事にこれがどう役立つのか、どうやったら役立てられるのか、もやもやしているなんてことがあるかも。またせっかく、紹介ページまで来たのに、短い説明ではイメージがわかず、スルーされてしまうかもしれないので、このブログで、実際の仕事でありそうなデーターを使って、こういう風にデーターを解析していけば、早く問題を解決できるのでは、という手順を紹介します。サイン曲線を表示したり、渦巻きを表示したりするのは楽しいですが、仕事と直接関係は無いですからね。（ここまでが前置き）

　

はじめまして

　はじめまして。
　ここは、失業中のメカ屋が適当なことを、書いているブログです。なるべくメカ屋っぽいことを書いて、メカ屋がどういうことを考えているのかを、理解される手助けになればと思います。まあ、私がメカ屋の代表というわけでもありませんけどね。
　せっかく、見に来ていただいたのでお土産を用意しました。

グラフマニア.ｘｌｓ

　データーを解析するための、エクセルファイル（テンプレート）です。日々データーの山に埋もれ、グラフをいっぱい書いている人にお勧めです。ぶっちゃけ、ピボットテーブルに何故散布図もしくは分布グラフを書く機能がないのか、とがっかりしている人に、ぴったりです。そんな人がどれほどいるか解りませんが、データーベース形式の表さえあれば、もう散布図は出来たも同然です。後は軸の表示を切り替えて、見たい要素の相関をチェックすることができます。

　あなたの仕事のお役にたてば幸いです。